Pythagorovu větu můžeme zapsat vztahem c² = a² + b², kde c označuje délku přepony pravoúhlého trojúhelníka a délky odvěsen jsou a, b.Pythagoras byl také zakladatelem pythagorejské školy, která se věnovala studiu matematických a filosofických otázek. Vztah Pythagorovy věty lze vyjádřit jako c² = a² + b². Tento vzorec říká, že obsah čtverce sestrojeného na přeponě pravoúhlého trojúhelníku je roven součtu obsahů čtverců sestrojených na jeho odvěsnách.umime.to/FV2
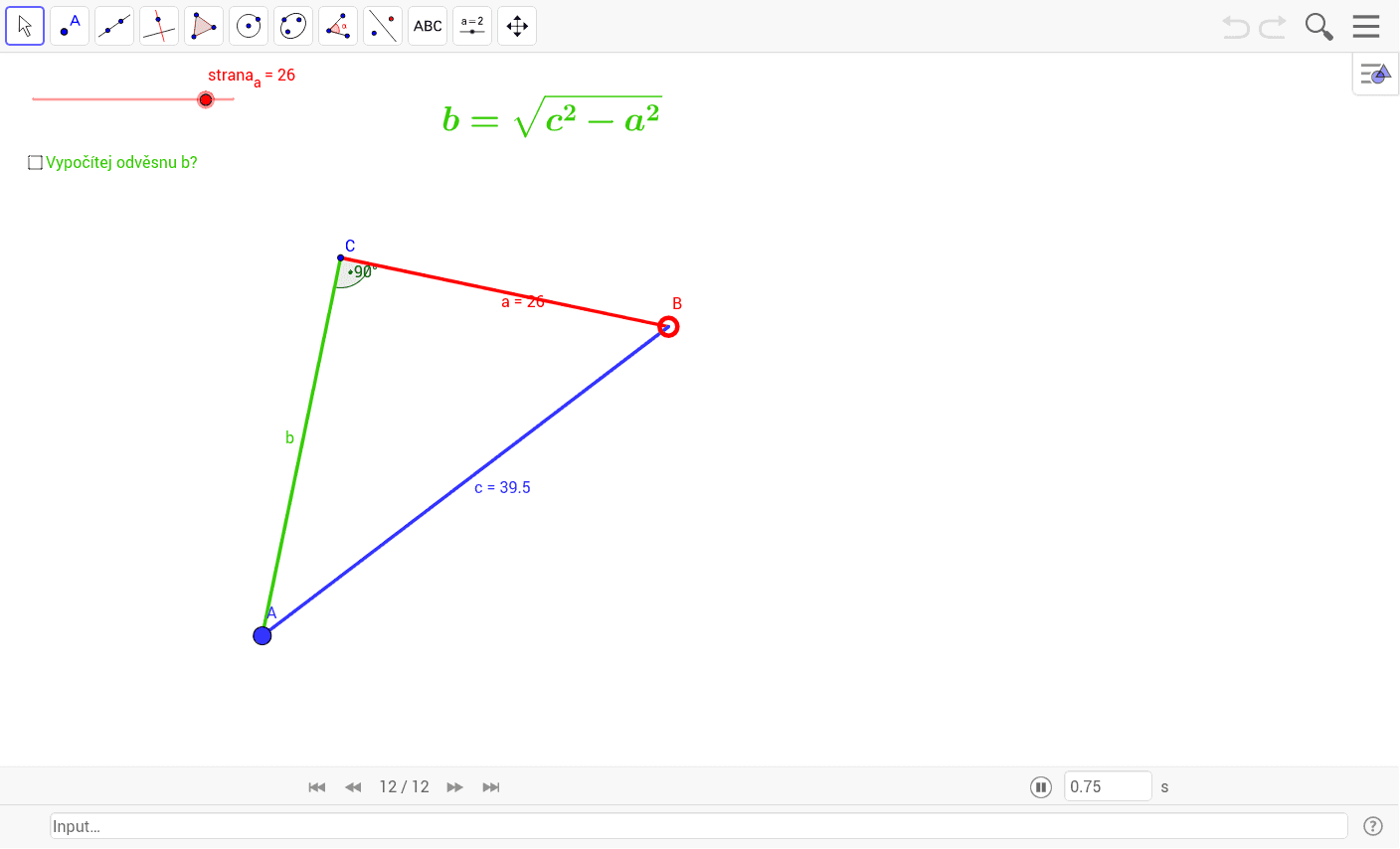
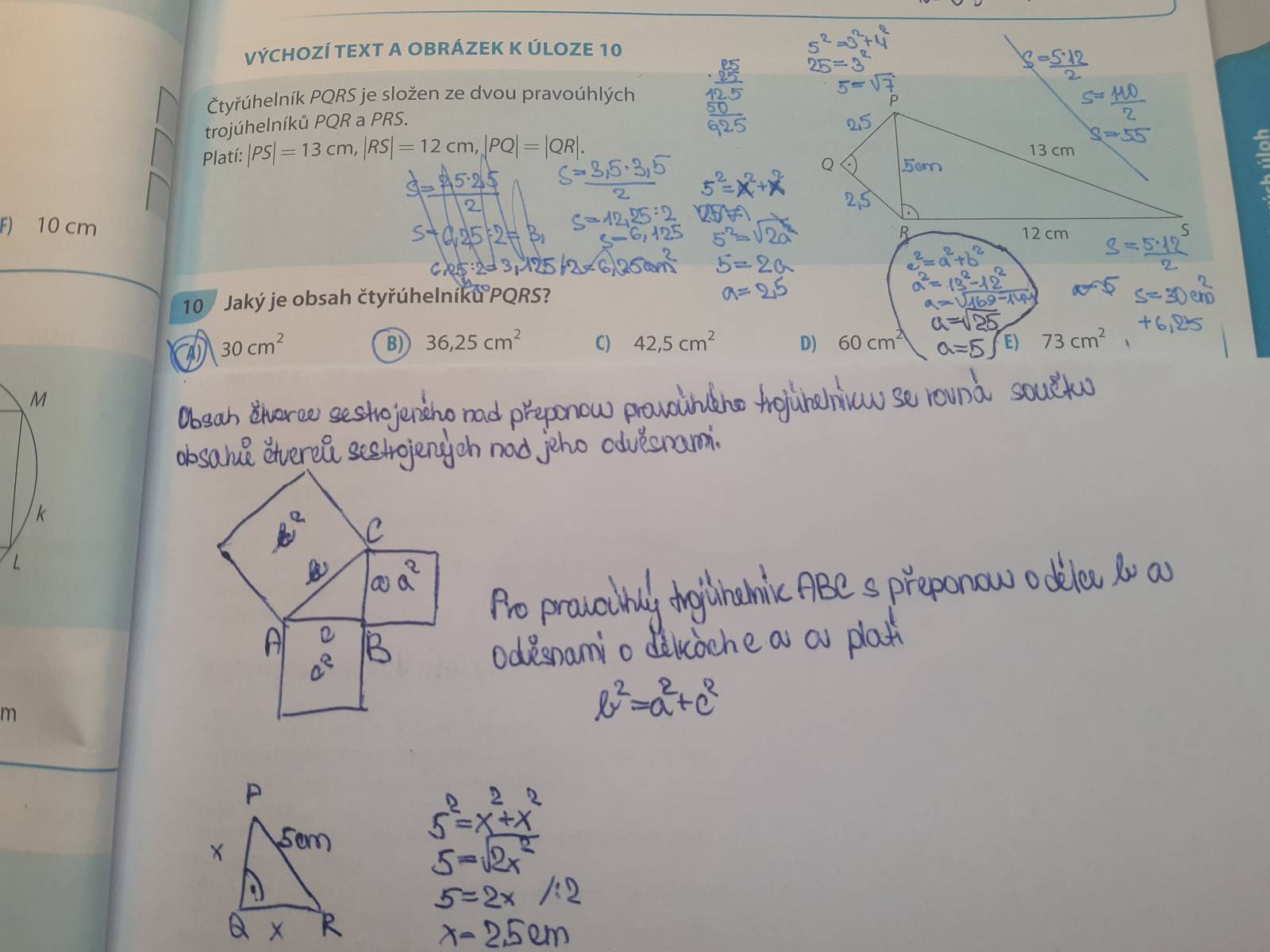
Věta zní: Obsah čtverce sestrojeného nad přeponou pravoúhlého trojúhelníku je roven součtu obsahů čtverců nad oběma jeho odvěsnami. Pythagorovu větu můžeme zapsat vztahem c 2 = a 2 + b 2 c^2 = a^2 + b^2 c2=a2+b2, kde c označuje délku přepony pravoúhlého trojúhelníka a délky odvěsen jsou a, b.
Jak zjistit Preponu : Přepona pravoúhlého trojúhelníku je vždy ta strana, která se nachází naproti pravému úhlu. Tato strana je v trojúhelníku nejdelší. Další dvě strany jsou nazvány protilehlá a přilehlá odvěsna.
Jak se počítá délka Odvěsny
Pythagorova věta umožňuje dopočítat délku třetí strany pravoúhlého trojúhelníka, u kterého známe délky dvou zbývajících stran:
- Délka přepony c = a 2 + b 2 c = \sqrt{a^2 + b^2} c=a2+b2 .
- Délka odvěsny a = c 2 − b 2 a = \sqrt{c^2-b^2} a=c2−b2 .
Co je to Odvesna : Nejdelší strana v pravoúhlém trojúhelníku se nazývá přepona. Přepona leží proti pravému úhlu. Zbývající dvě strany nazýváme odvěsny.
Pythagorova věta umožňuje dopočítat délku třetí strany pravoúhlého trojúhelníka, u kterého známe délky dvou zbývajících stran:
- Délka přepony c = a 2 + b 2 c = \sqrt{a^2 + b^2} c=a2+b2 .
- Délka odvěsny a = c 2 − b 2 a = \sqrt{c^2-b^2} a=c2−b2 .
Pythagorás ze Samu
První Řek, který si uvědomil, že Večerka i Jitřenka jsou jedna a tatáž planeta – Venuše. Prohlásil, že Země je kulatá a rozšířil Anaximandrův model sfér. V matematice proslul Pythagorovou větou pro pravoúhlý trojúhelník (kvadrát velikosti přepony je roven součtu kvadrátů velikostí odvěsen).
Jak se počítá Délka odvěsny
Pythagorova věta umožňuje dopočítat délku třetí strany pravoúhlého trojúhelníka, u kterého známe délky dvou zbývajících stran:
- Délka přepony c = a 2 + b 2 c = \sqrt{a^2 + b^2} c=a2+b2 .
- Délka odvěsny a = c 2 − b 2 a = \sqrt{c^2-b^2} a=c2−b2 .
Nejdelší strana v pravoúhlém trojúhelníku se nazývá přepona. Přepona leží proti pravému úhlu. Zbývající dvě strany nazýváme odvěsny. Odvěsny svírají pravý úhel.Obvod je součet délek čar, které útvar vymezují. Obvod se měří v jednotkách délky.
Pythagorova věta umožňuje dopočítat délku třetí strany pravoúhlého trojúhelníka, u kterého známe délky dvou zbývajících stran:
- Délka přepony c = a 2 + b 2 c = \sqrt{a^2 + b^2} c=a2+b2 .
- Délka odvěsny a = c 2 − b 2 a = \sqrt{c^2-b^2} a=c2−b2 .
Jak se pozna pravý úhel : Pravý úhel je úhel, který tvoří polovinu přímého úhlu či čtvrtinu plného úhlu. Jeho numerická hodnota ve stupních je 90, v radiánech π/2. Název pravý úhel vznikl nepřesným překladem latinského termínu angulus rectus, kde ovšem slovo rectus bylo původně použito ve významu „vzpřímený“, nikoli „pravý“.
Jak dlouho žil Pythagoras : Πυθαγόρας ο Σάμιος, okolo 570 př. n. l. ostrov Samos – po 510 př. n. l. Krotón v jižní Itálii) byl řecký filozof, matematik, astronom i kněz.
Co vymyslel Pythagoras
V tomto ohledu Pythagoras první použil matematiku ve službách fyziky! Do obecného povědomí vešla především tzv. Pythagorova věta o „součtech čtverců“ stran v pravoúhlém trojúhelníku. Ono c2 = a2 + b2 zná bez nadsázky téměř každý.
Pro výpočet obsahu trojúhelníku použijeme vzorec obsah = (strana krá výška)/2.Závěrem je, že obvod kruhu o se určí ze vzorce o = πd, kde d je průměr kruhu, nebo o = 2πr, kde r je poloměr kruhu. Žáci by měli odhalit princip Archimédova postupu – totiž, že čím více stran má n-úhelník, tím více se jeho délka blíží délce kružnice (obvodu kruhu) s průměrem odpovídajícím úhlopříčce n-úhelníku.
Jak vypočítat délku strany obdélníku z obvodu : Obvod vydělíme počtem dílků a získáme hodnotu jednoho (60 : 10 = 6). Délka jedné strany je (počet dílků * hodnota jednoho dílku) 2 * 6 = 12 , 3 * 6 = 18.